Math 1B  Calculus II  Chapter 6 test (1) Solutions  fall ’06

 

1.      Consider the area of the region bounded by  and .

a.       Sketch a graph illustrating the region.
ANS: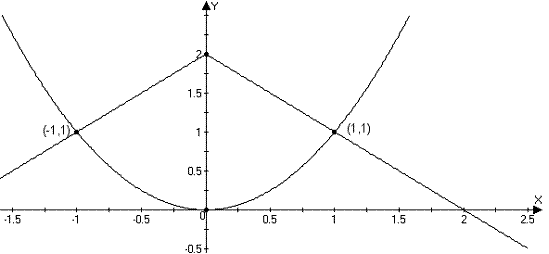

b.      Compute the area by integrating over x and using symmetry, as appropriate.
ANS:  Since the region is symmetric about the y-axis,  

c.       By integrating over y and splitting the region into 2 pieces, as appropriate.
ANS: 

2.      Consider the area of the region bounded by  and .

a.       Sketch a graph illustrating the region.
ANS: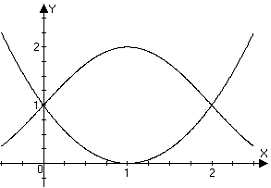 

b.      Compute the volume of revolution generated by revolving the region about the x-axis. 
Use either the shell method or the washer method, whichever seems easier.
ANS:  The disk method is easiest here: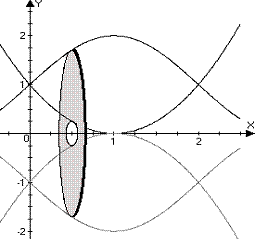
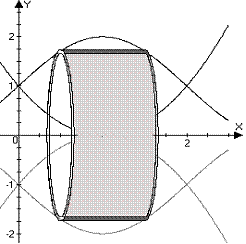
The shell method yields
.  Substituting u = y  1  in this last integral we get
Integrating by parts once, we get 
For  use  to get 
whence, adding the integral to both sides of the equation,
 and
Putting these together we have  

c.       Compute the volume of revolution generated by revolving the region about the y-axis. 
Use either the shell method or the washer method, whichever seems easier.

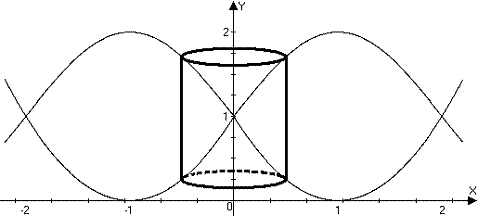
ANS:  The shell method is easier here:

Using the washer method, we’d have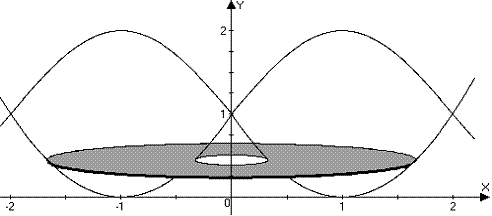

3.      A hole of radius r is drilled through the center a sphere of radius R > r.  Find the volume of the remaining portion of the sphere.
ANS:  The cross-section of the sphere in the x-y plane has the equation .   Suppose the drilling is done parallel to the y axis, then the x coordinate of the upper lip in the x-y plane is r and the y coordinate is .  The volume as illustrated  
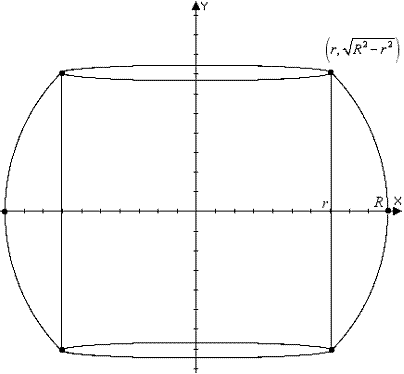
The volume can be computed using washers by
Using shells, we’d have .  Substituting  we have  and the integral becomes
Using washers, we’d have

4.      Consider the curve in the x-y plane described by the parametric equations

                                                      

a.       Tabulate values of t, x, and y for t ranging from  to .
SOLN:   

b.      Plot these points in the x-y plane and sketch the curve.
ANS:

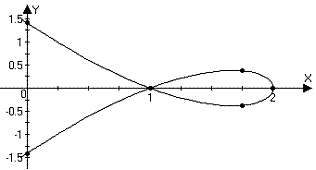
c.       Compute the area of the loop formed by this curve.  Integrate over t.
ANS:  Using symmetry, we see that a vertical cross-sectional length is 2|y|.
 

d.      Compute the arc length of the loop.  Integrate over t.
ANS: 
Unfortunately, there is no elementary antiderivative, so we must resort to numerical methods such as using the the TI-200:

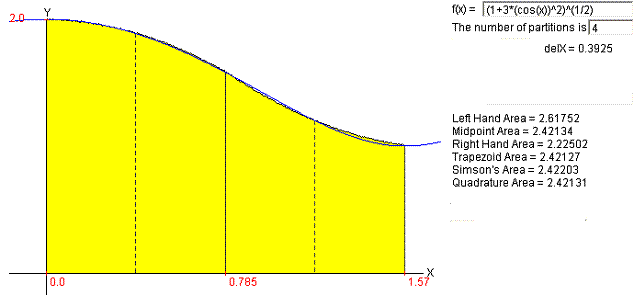
5.      Use Simpson’s rule with n = 4 to estimate the arc length of the parametric curve
                                              . 
for .  Note: there is no elementary antiderivative, so the approximation is appropriate.
Compare your answer with the value of the integral produced by your calculator.
ANS:  arc length =
 

devisive